Dimensional Changes in Wood
From early Paleolithic times, wood has been one of the most important raw materials for making everything from furniture to weapons to art. The availability of metal tools about 5000 BC gave Egyptians the ability to improve the art of cutting veneer pieces to use in construction of various products. Although wood uses and processing techniques have been developing for millennia, the science of wood technology is relatively new.
Wood is a hygroscopic material which loses and gains moisture as a result of changes in humidity. Hygroscopicity is one of the most distinctive properties of wood. Any kind of wood product will absorb and desorb moisture from the surrounding air until it reaches equilibrium moisture content, a balance point between the wood’s moisture content and that of the surrounding environment. Hygroscopic materials such as wood and other lignocellulosic material change their dimensions with fluctuations in relative humidity. Therefore, determination of moisture content of wood products before they are used is an important task. Based on the current moisture content of wood and its surrounding conditions, dimensional changes in wood will take place, influencing its effectiveness as a construction material.
Water in wood
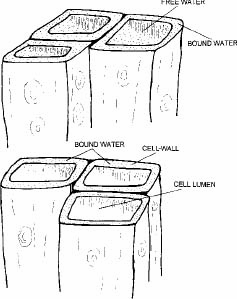
Water in freshly cut harvested wood is located within the cell wall and the cell lumen. Water found in the cell wall is called bound water, while water in the lumen is referred to as free water. (See Figure 1.) Free water is quite simple to remove; as soon as a tree is cut, free water begins to evaporate. The water in the cell wall is held by adsorption force which involves the attraction of water molecules to hydrogen bonding in cellulose, hemicellulose, and lignin.
Figure 1. Location of water in a cell.
The amount of water in wood is referred to as its moisture content (MC) and is defined as weight of the water present, expressed as a percentage of the moisture-free or oven dry weight of the wood. MC can be determined using various methods. Standard oven dry methods and electrical moisture meters are the most commonly used techniques. Chemical and distillation methods can also be used to determine moisture content of wood; however, they are usually confined to laboratory use.
The most accurate technique to measure MC of wood is the oven dry method. Individual
specimens of wood to be tested are weighed on a balance and placed in a ventilated
oven set at just above the boiling point of water, 103± 2 C (219 F). Samples are
kept in the oven until they reach a constant weight, which usually takes 24–48 hours.
The new weight is called oven dry weight and is then used to calculate MC in the sample.
MC calculated in this way could be over 100 percent because the denominator in the
equation is the dry weight, not the total weight. By way of example, if a 3 x 3 x
5-inch oak sample weighs 1.0 lb. and its oven dry (OD) weight is 0.70 lb., its MC
is :
MC = Weight (M) – Weight (OD) ÷ Weight (OD) x 100
MC= [(1.0-0.7) ÷ 0.7] 100 = 42.8%
Shrinkage and swelling of wood
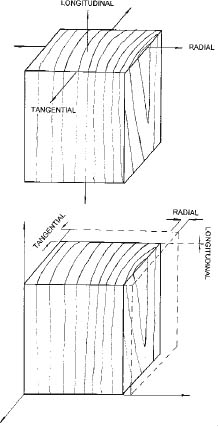
Dimensional changes, shrinkage, and swelling in wood take place below the fiber saturation point (FSP) where all of the water exists only within the cell wall (Figure 1). For simplicity, shrinkage and swelling will be combined and referred to collectively as shrinkage here. Shrinkage is proportional to the amount of water exchanged between a piece of wood and its environment. Wood is an anisotropic material; that is, its dimensions change differently in three directions: tangentially, radially, and longitudinally. Tangential dimensional change has the highest rate of change due to parallel orientation of microfibrils along the axis of the cell wall. Shrinkage in the radial direction is the second largest, while longitudinal shrinkage is negligible for most practical applications. A schematic approach to the swelling of a block in three directions is shown in Figure 2. In general, dimensional change is expressed as percent and can be calculated using the following formula:
Shrinkage or swelling (%) = Change in dimension or volume ÷ Initial dimension or volume x 100
Dimensional changes can also be estimated based on the following equation:
DC = OD x SV x (CMC ÷ FSP) x 100
where DC is dimensional change due to change in moisture content (CMC), OD is original dimension, SV is shrinkage value from green to oven dry moisture content, and FSP is fiber saturation point, which is considered 28 percent for practical purposes. Table 1 displays shrinkage and swelling values from green to oven dry moisture content for some of the most commonly used species.
Figure 2. Swelling of a block in three directions.
Table 1. Tangential and radial shrinkage values from green to oven dry moisture content.
| Species | Tangential | Radial |
|---|---|---|
| (%) | (%) | |
| American Elm | 9.5 | 4.2 |
| Sugar Maple | 9.9 | 4.8 |
| Black Oak | 11.1 | 4.4 |
| Red Oak | 8.9 | 4.2 |
| White Oak | 10.5 | 5.6 |
| Black Walnut | 7.8 | 5.5 |
| Yellow Poplar | 8.2 | 4.6 |
| Black Cherry | 7.1 | 3.7 |
| Sweetgum | 10.2 | 5.3 |
| Eastern Redcedar | 4.7 | 3.1 |
| Western Redcedar | 5 | 2.4 |
| White Fir | 7.1 | 3.2 |
| Eastern Hemlock | 6.8 | 3 |
| White Pine | 7.4 | 4.1 |
| Ponderosa Pine | 6.2 | 3.9 |
| Redwood | 4.5 | 2.5 |
| Spruce | 7.5 | 4.3 |
| Balsa | 7.6 | 3 |
| Ramin | 8.7 | 3.9 |
| Teak | 4 | 2.2 |
| Mahogany | 5.1 | 3.7 |
There is a direct relationship between density of wood and shrinkage values. Species with higher density shrink more than those with lower density. Even though shrinkage values of many species are relatively low, they still play a significant role in designing wood structures. If shrinkage of wood is not taken into consideration during the design stages, certain construction defects such as warping, cracking, and buckling may easily occur, lowering the overall quality of the finished product.
If we assume that lumber production in the U.S.A. is approximately 40 billion board-feet
per year on average, and assuming volumetric shrinkage due to moisture content change
of four percent, we would expect to lose 1.6 billion board feet of material per year.
This hypothetical example emphasizes the importance of accounting for shrinkage in
wood products.
Dimensional stabilization of wood is needed for special applications. Thermosetting resins that are highly water resistant are normally used for this purpose. There have been many studies aimed at stabilizing the cell wall so that shrinkage of wood can be controlled. Resin–treated wood, resin-treated compressed wood, untreated compressed wood, wood treated with polyethylene glycol, and wood polymer composites are some of the means used to reduce or eliminate cell wall shrinkage. However, none of these methods has been put into practical use due to economical and technical considerations.
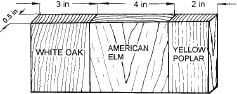
When shrinkage values of different species are taken into design consideration, disadvantageous characteristics of wood can be handled properly. Figure 3 shows a hypothetical panel consisting of three species in both radial and tangential grain orientation.
Figure 3. Each piece will have a different swollen length due to its grain orientation when overall moisture content of the construction is increased 10%. Swollen length of the panel is a function of moisture content change and physical properties of species.
If this construction has an average moisture content of 5 percent and its moisture is increased to 15 percent, swollen length of the panel can be estimated as follows:
White oak : 3 x 0.056 x (0.10 ÷ 0.28) = 0.060 in.
American elm : 4 x 0.095 x (0.10 ÷ 0.28) = 0.135 in.
Yellow poplar : 2 x 0.046 x (0.10 ÷ 0.28) = 0.033 in.
The length of the panel after exposure to higher moisture will be :
9 + 0.060 + 0.135 + 0.033 = 9.228 in.
If this panel were restrained on a wall under these moisture conditions, buckling could occur unless a gap is left within the framework of the panel.
Conclusion
Wood will shrink and swell as the result of moisture content change in the surrounding environment. Shrinkage of wood and wood products is one of the most important design parameters to consider in order to eliminate future defects in the product. As long as this inherent problem is properly treated, one of our most important renewable materials can be used efficiently for many applications without major problems.
Salim Hiziroglu
Assistant Professor, Wood Products