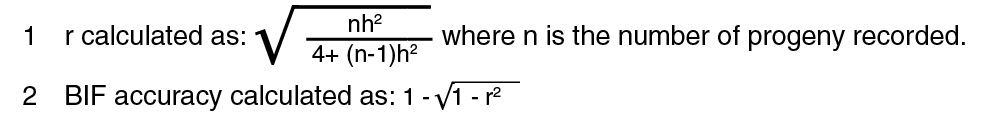Understanding EPD Accuracies
EPDs, or Expected Progeny Differences, are an important part of both sire and replacement heifer selection in the beef industry. But just knowing the animal’s EPD for a particular trait is not the only information to consider when making these important decisions. In making selection decisions, one always wants to select the animals, whether bulls or females, that have the best genetic merit for a combination of traits that will maximize profitability in the cowherd. While EPDs do provide one of the best methods to select animals for their value as parents of the next generation, the true breeding value of an animal cannot be known with 100 percent certainty, which is why understanding EPD accuracy values is an essential part of sire and replacement heifer selection.
An EPD is always paired with a corresponding accuracy value (see Table 1) which ranges
from 0 to 1 (Please note that accuracies are sometimes expressed as the accuracy multiplied
by 100; for example, an accuracy of 0.15 may be listed as 15). This value reflects
the confidence in the genetic merit prediction. An accuracy of 0 would reflect no
confidence in the estimate, whereas an accuracy of 1 would reflect complete confidence
that the true breeding value was known. In practice, accuracy values do not appear
with values that extreme (either no or complete confidence).
Table 1. EPD estimates with their corresponding accuracies.
| Trait | CED | BW | WW | YW | MA | SC |
|---|---|---|---|---|---|---|
| EPD | 10 | 1.3 | 25 | 54 | 6 | -0.1 |
| Acc | 0.15 | 0.23 | 0.26 | 0.12 | 0.05 | 0.14 |
PAEPDprogeny = 1/2 EPDSire + 1/2 EPDDam
EPDprogeny = 1/2 EPDSire + 1/2 EPDDam + φ
Figure 1. Parent average EPD (top) observed when an animal is born compared to a true progeny EPD (bottom).
When animals are born, they have a low accuracy EPD that is formed from the average
of the parent’s EPD values (Figure 1, top). Most breed associations will automatically
assign a small amount of accuracy to that prediction, sometimes 0.05. Other associations
will denote a parent average EPD by assigning a P for that accuracy. Because of this,
full-sibling flush mates will all have the same parent average EPD for all traits
when they are born. You may recall from biology class that genes assort independently
when gametes1 are formed. Independent assortment2 means that each gamete has an independent assortment of genes that could be better
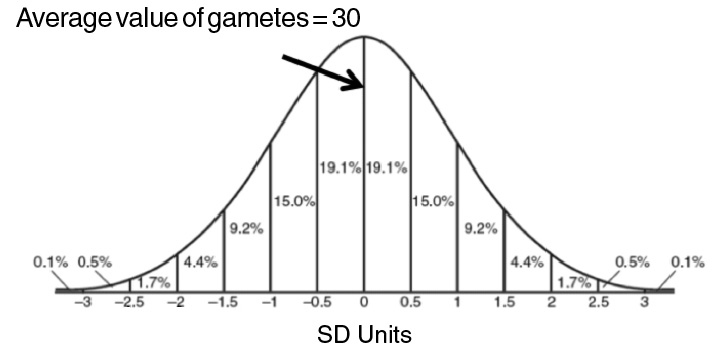
or worse than the average gamete. Most gametes will be close to average (Figure 2),
however, some will receive very favorable and some very unfavorable assortments.
As a result, we need a third term in the equation (See Figure 1, bottom), φ, called
the Mendelian sampling term which describes whether the animal received a better or
worse than average sampling of genes from its parents. The true value of this term
cannot be estimated until we have additional information, typically phenotypic3 records from the individual and its relatives.
Figure 2. The genetic value of most gametes will be near the mean.
Because higher accuracy correlates to more confidence in the prediction, it is useful
to be cognizant of methods in which to build accuracy in young sires and replacement
heifers. Accuracy is dependent on several different factors including trait heritability,
number of phenotypic records on the individual and its relatives, and number of records
on any traits that are genetically correlated4. Because the heritability cannot be
influenced directly, recording the phenotypic performance of the individual in question
and its progeny is the easiest way to build accuracy for an EPD on a particular trait
(See Table 2). Because close relatives also share many of the same genes, phenotypic
records on relatives also contribute towards accuracy. Genomic information is now
used in the genetic evaluations for Angus, Hereford, and Simmental cattle. It will
be used in many other breeds as the use of the technology progresses. The addition
of genomic information on an animal into genetic evaluation performed by the breed
associations is another way to build accuracy in unproven animals. The amount of
increase in accuracy is proportional to the genetic variance that is explained by
the marker panel5-the more variance explained, the larger the increase in accuracy.
Table 2. Approximate number of progeny records needed to obtain a specified accuracy level.
| Heritability (h2) | ||||
|---|---|---|---|---|
| “True” Accuracy (r)1 | BIF Accuracy2 | Low (0.1) | Moderate (0.3) | High (0.5) |
| 0.1 | 0.01 | 1 | 1 | 1 |
| 0.2 | 0.02 | 2 | 1 | 1 |
| 0.3 | 0.05 | 4 | 2 | 1 |
| 0.4 | 0.08 | 8 | 3 | 2 |
| 0.5 | 0.13 | 13 | 5 | 3 |
| 0.6 | 0.2 | 22 | 7 | 4 |
| 0.7 | 0.29 | 38 | 12 | 7 |
| 0.9 | 0.4 | 70 | 22 | 13 |
| 0.999 | 0.99 | 3800 | 1225 | 700 |
When using genomic panels, it is useful to be mindful of where the most benefit related to increase in accuracy can be realized. The higher the initial accuracy of the EPD, the smaller the increase in accuracy will be from running a genomic panel. The general rule of thumb is that genomic tests are most useful on sires or dams that have no progeny recorded, and in some cases the genomic test can be equivalent to several progeny records (2 to 20).
Upon examination of Table 2, you will notice that the accuracy is specified two ways:
one denoted the “true accuracy” and the other denoted as BIF6 accuracy. In its strictest
definition, accuracy is the correlation of the true breeding value with the predicted
breeding value (keep in mind that an EPD is 1/2 of the breeding value). Accuracies
for genetic evaluations can be denoted by many different names, including accuracy
(r), reliability (r2), or the BIF accuracy. Each value can be converted into the other,
and the main difference between the numbers is how they are scaled. Accuracy (r) tends
to be the highest value, whereas BIF accuracies are scaled down to smaller values
(Table 2).
A practical way to think about EPD accuracies is the possible change in an EPD given
a specific accuracy. Many breed associations publish possible change tables as part
of their sire summaries and they are often found in the same section as the EPD percentile
ranking tables. To illustrate this concept, consider two bulls which both have a birth
weight EPD of 1.2 (Table 3). The unproven sire’s EPD has a much larger possible change
value than the proven bull. This means that he may sire progeny with considerably
lower birth weights than previously thought, or his EPD may trend towards having a
higher birth weight as we record additional progeny records. The proven bull’s EPD
will be much more stable over time as additional progeny are recorded, as there is
already high confidence in the estimate listed.
Knowing the amount that an EPD can change over time as accuracy increases is a very
useful tool for risk management. Using a bull that may not have EPDs that are as impressive
as a new yearling bull, but that have high accuracies is a reasonable choice to limit
risk. Use of an artificial insemination program is one of the most effective ways
to locate and incorporate genetics from proven bulls into the cowherd. For those producers
less adverse to risk, the younger, unproven sire offers the opportunity to find a
vastly superior bull with the newest genetics, while simultaneously absorbing the
risk that the EPDs for that sire may change and he may not be as impressive as initially
estimated. A good strategy for herds large enough to breed to several sires throughout
the breeding season is to balance their risk. Many producers may want to use several
proven herd sires coupled with some newer genetics (younger herd sires) to help balance
the risk of their breeding decisions within their herds with the need to make genetic
progress.
Table 3. Possible change values and true EPD ranges for two bulls with the same birth weight EPD, but with different accuracies.
| Sire | EPD | Accuracy | Possible Change | True EPD Range (68% Confidence) |
|---|---|---|---|---|
| 1 (unproven) | 1.2 | 0.1 | ±2.7 | -1.5 to 3.9 |
| 2 (proven) | 1.2 | 0.8 | ±0.6 | 0.4 to 2 |
Understanding both EPDs and their associated accuracies is an important step towards making appropriate breeding decisions within the cowherd while simultaneously managing risk within the production operation.
Vocabulary:
- Gamete – A cell generated for sexual reproduction such as a sperm or egg. The process of producing a gamete is called meiosis.
- Independent assortment – Process whereby alleles segregate independently during the formation of gametes (meiosis).
- Phenotypic – The physical performance or appearance of an animal (a phenotype).
- Genetically correlated – The proportion of variance that two variables share due to genetic causes. For example, many genes that control growth at weaning also have an effect on growth at yearling, meaning the two traits are genetically correlated.
- Marker panel – A set of genetic markers (SNPs or microsatellites) that are used to genotype an animal.
- BIF – Acryonym for Beef Improvement Federation. To learn more about BIF, visit www.beefimprovement.org.
Megan Rolf
Former Assistant Professor