Strength Properties of Wood for Practical Applications
Mechanical properties of wood play an important role when used for different design applications. Wood is widely used for structural purposes. This fact sheet summarizes some of the basic concepts related to mechanical characteristics of wood, including viscoelasticity, compression, shear, bending strength properties and how such characteristics should be taken into consideration for an efficient practical design.
Viscoelasticity
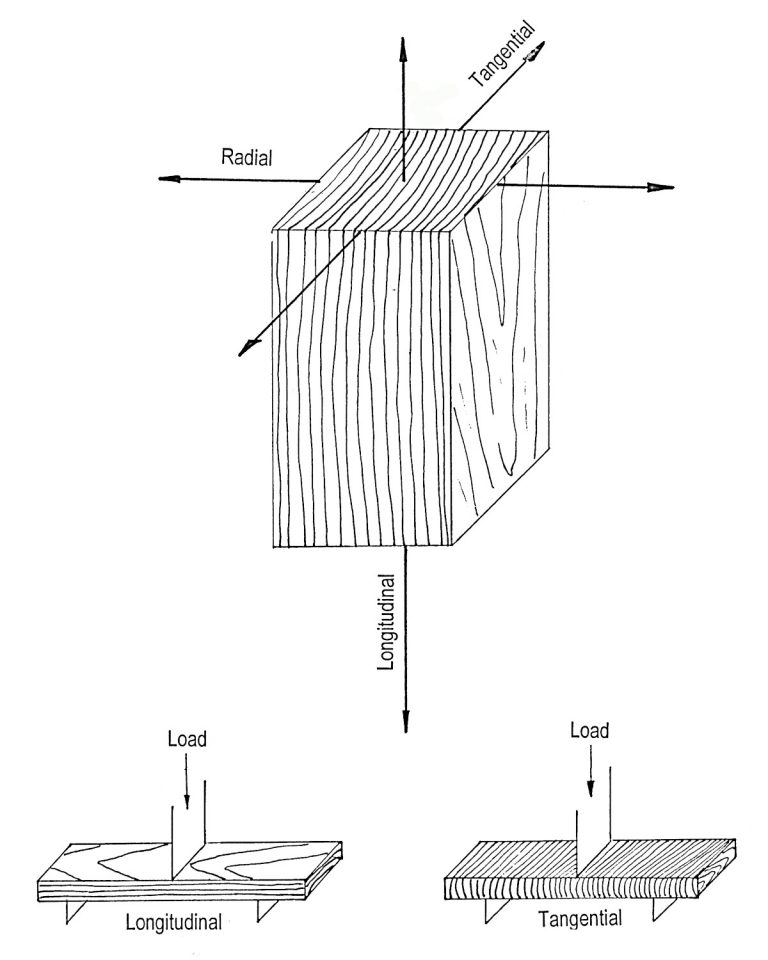
In contrast to metals and plastics, wood is an orthotropic material, meaning its properties will be independent in three directions – longitudinal, tangential and radial, as illustrated in Figure 1. Another unique property of wood is its viscoelasticity, which can be described as having both plastic and elastic characteristics when exposed to a certain deformation.
Figure 1. Orthotropic structure of wood.
Elastic materials easily stretch under an applied load. However, they return to their original conditions once the load is released. In contrast, plastic materials stay at the stretched condition even if the load is released after a long period time. The behavior of wood products is between the above two types of conditions.
A bookshelf example can be used to illustrate the viscoelasticity of wood: A number of books are put on a shelf and, in time, it will have a limited amount of sagging deformation. When all books are removed from the shelf, it will never return to its original flat condition. Thus, there will be a residual deformation left because of its viscoelasticity. Figure 2 illustrates the viscoelastic behavior of wood, as in the bookshelf example.
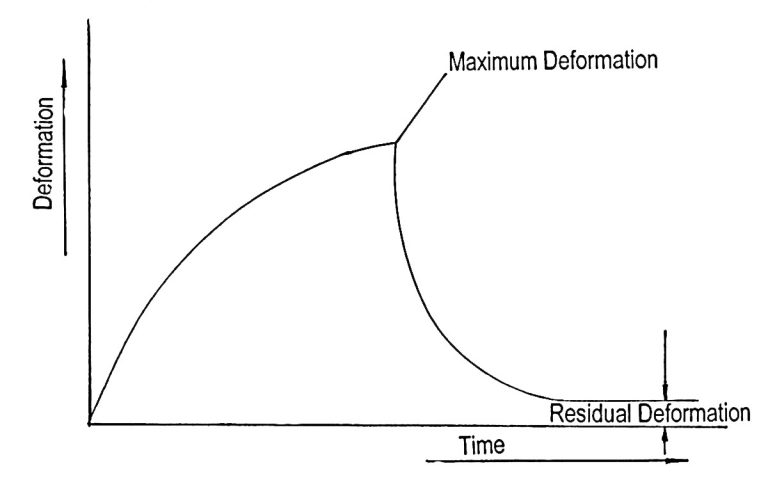
Figure 2. Viscoelastic behavior of wood.
Compression
Compression of wood and wood-based materials plays an important role in almost any construction projects. If the compression strength or bending strength of a 2-inch by 4-inch beam is not known, deflection due to bearing a load may cause significant deformation, which could even lead to its failure during service life. Therefore, most softwood construction lumber is graded based on allowable load resistance, which can be determined from a stress test. However, strength properties of hardwood lumber are not that critical because a majority of it is used for furniture manufacturing and is not exposed to substantial loads.
Compression or shear strength of a wood beam or truss used extensively for construction can be calculated based on the following equation:
Sigma (σ) = P/A, where σ is stress, P is load and A is surface area.
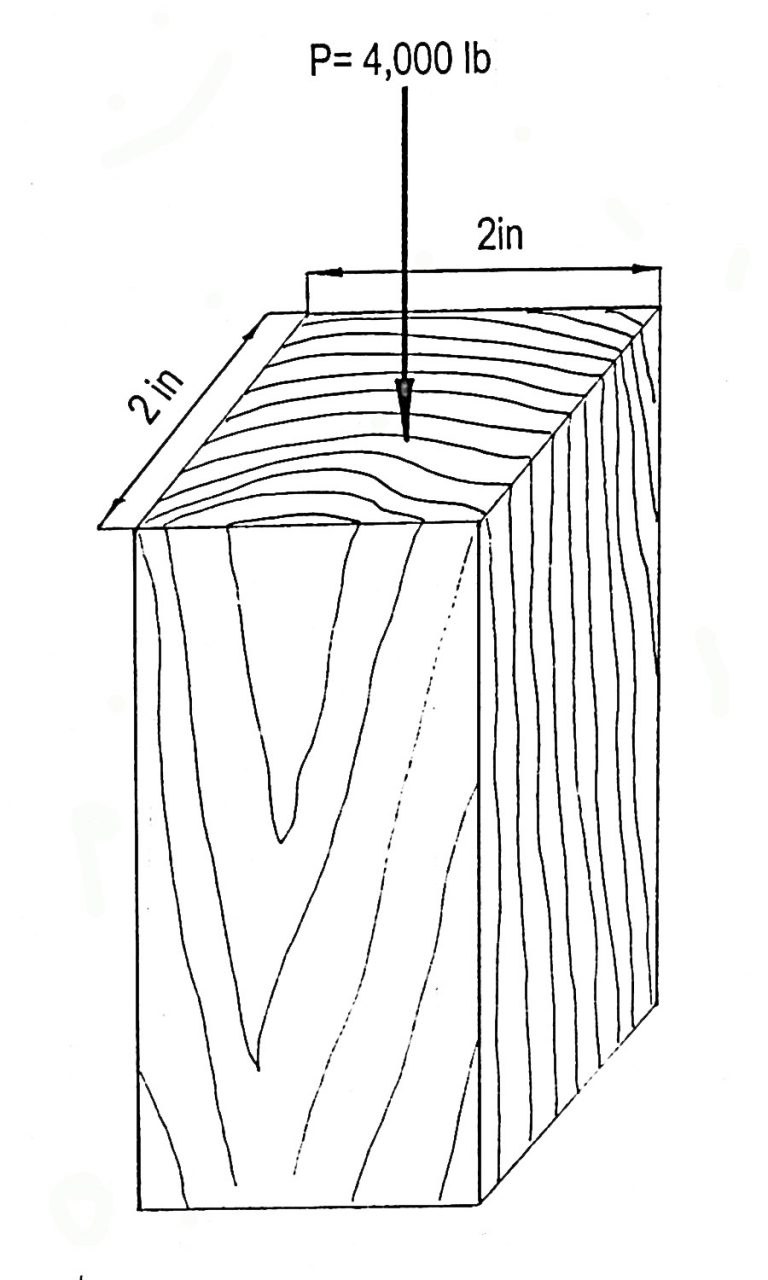
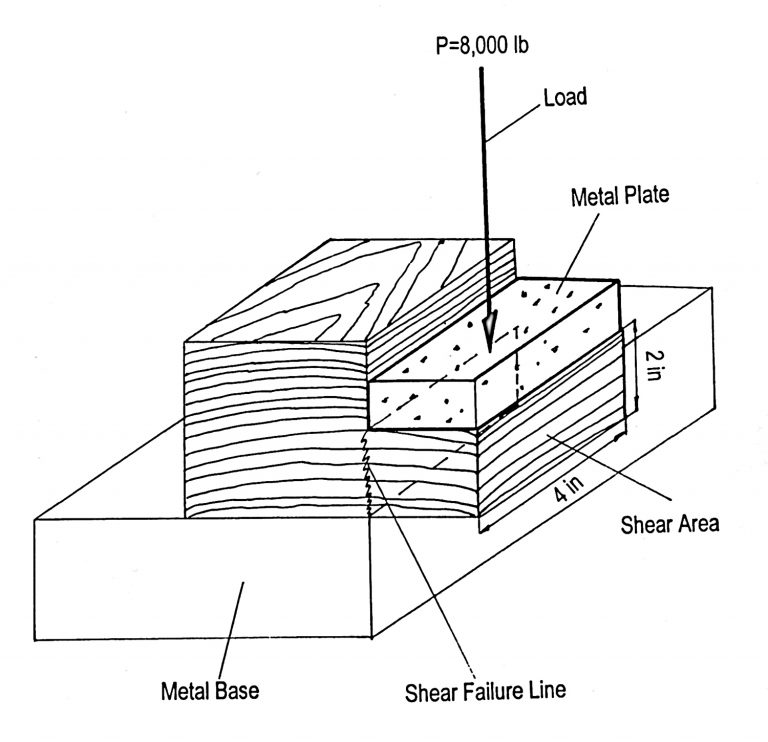
In general, stress is the load per unit area and is expressed in pound per square inch (psi), kilogram per square centimeter (kg/cm2) or any other units. Figures 3 and 4 show compression and shear stress developed by a perpendicularly applied load on small wood blocks.
Figure 3. Compression parallel to grain.
Figure 4. Sheer stress of a sample.
MOE and MOR
In the case of bending a beam, we are dealing with modulus of elasticity (MOE) and modulus of rupture (MOR) to evaluate its load resistance. While MOE is a measure of the stiffness of a body, MOR is related to maximum strength that can be resisted by a member. Both are expressed as stress similar to most of the other mechanical properties of wood. The following two equations are used to calculate MOE and MOR of wood with a rectangular cross section:
MOE = (P L3) / (48 I D)
MOR = (Pmax L) / (b d2)
I = (bd3) / 12
Where:
P = load below proportional limit (lb.)
Pmax = failure load (lb.)
L = test span (in.)
b = width of the sample (in.)
d = thickness of the sample (in.)
D = center deflection (in.)
I = moment of inertia, which is the inertia of a rigid body with respect to its rotation and, in the case of a rectangular cross section, is expressed as in4.
In general, depending on the species, wood has MOE and MOR values of 800,000–2,500,000 psi and 5,000–15,000 psi, respectively. If a Red Oak with an approximate MOE value of 2,000,000 psi is used to make the bookshelf mentioned above, its deflection deformation will be less than that of Aspen, which has a lower MOE.
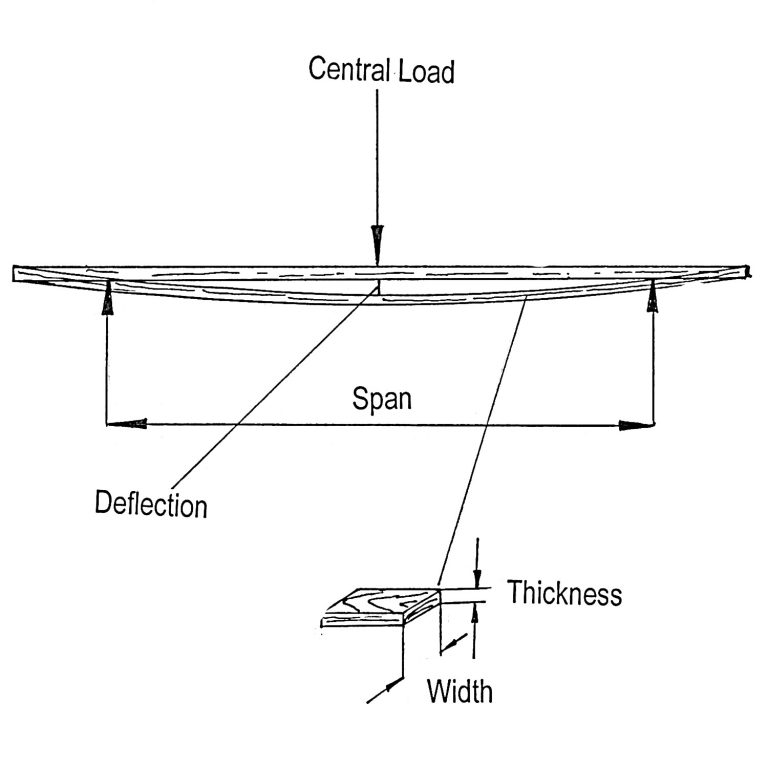
Both MOE and MOR values of different species can be obtained from various references for a particular design. Table 1 displays some of the mechanical properties, including MOE and MOR, of several species. Figure 5 also illustrates a typical beam bending with deflection as a result of a central load.
Table 1. Some of the mechanical properties of various species at 12 percent moisture content. (From Wood Handbook, 1999)
| Species | MOE (psi) | MOR (psi) | Compression // to the grain (psi) | Sheer // to the grain (psi) | Specific gravity |
|---|---|---|---|---|---|
| Douglas Fir | 1,950,000 | 12,400 | 3,780 | 900 | 0.48 |
| Sitka Spruce | 1,570,000 | 10,200 | 5,610 | 1,150 | 0.40 |
| White Pine | 1,240,000 | 8,600 | 4,800 | 900 | 0.35 |
| Eastern Redcedar | 880,000 | 8,800 | 3,520 | 1,010 | 0.47 |
| Red Pine | 1,630,000 | 11,000 | 6,070 | 1,210 | 0.46 |
| Cottonwood | 1,100,000 | 6,800 | 4,020 | 790 | 0.34 |
| Red Oak | 2,200,000 | 13,400 | 6,540 | 1,850 | 0.54 |
| Red Maple | 2,200,000 | 13,400 | 6,540 | 1,850 | 0.54 |
| White Oak | 1,030,000 | 10,300 | 6,060 | 1,820 | 0.64 |
| Black Walnut | 1,680,000 | 14,600 | 1,010 | 1,370 | 0.55 |
Figure 5. Bending of a wood beam.
Moisture Content
The moisture content of wood also is an important parameter influencing almost all mechanical properties. Strength properties of wood increase with its decreasing moisture content. For example, air-dried wood with average moisture content of 12-13 percent will have higher strength properties than that of wood with 20 percent moisture content. In general, wood is dried to 15-20 percent moisture for typical structural application rather than using it in green condition. Strength properties of wood also can be estimated using the following equation for given moisture content, so that wood can be used with a higher efficiency for any applications:
P = P12 (P12 / Pg) (12-M / Mp–12)
Where:
P = property value
P12 = property value at 12 percent moisture content
Pg = property value at green moisture content
M = moisture content
Mp = moisture content at which property is changed (Mp is assumed 25 percent for most species, based on USDA Forest Service, 1999).
Example: If a Douglas Fir beam has MOR values of 7,700 psi at green moisture content and 12,400 psi at 12 percent air-dry conditions, its MOR value at 18 percent moisture content can be calculated as below:
P = 12,400 (12,400 / 7,700) (-6 / 13)
P = 12,400 x 1.610 -0.461
P = 12,400 / (1.610) 0.461
P = 9,959 psi
Further Information
Detailed information about mechanical properties of wood and wood products also can be found in the following literature:
Wood Handbook (1999). Wood as an engineering material. USDA Forest Products Lab: Madison, Wisconsin.
Hoadley, B. (2000). Understanding Wood. The Taunton Press: Newtown, Connecticut.
Ambsore, J. (1994). Simplified Design of Wood Structures. John Wiley & Sons, Incorporated: New York.
Smith, I., Landis, E., & Gong, M. (2003). Fracture and Fatigue in Wood. John Wiley & Sons, Incorporated: New York.
Bowyer, J., Smulsky, R., & Haygreen, J. (2007). Forest Products & Wood Science, An Introduction. Blackwell Publishing Incorporated: Malden, Massachusetts.
Salim Hiziroglu
FAPC Wood Products Specialist